Violencia
La palabra violencia proviene del latín violetia, que significa "abuso de fuerza". Para los antiguos griegos, la violencia es arrogancia, es decir, abuso de poder, profanación de la naturaleza, así como transgresión de leyes sagradas. De hecho, en la Naturaleza nada es independiente de su contexto, un mismo fenómeno natural (lluvias torrenciales, tormentas, etc.) puede considerarse devastador en un momento y beneficioso en otro. Los mismos actos pueden tener significados opuestos según las situaciones en las que se encuentren y las intenciones...
Historia
Ciencia
Lengua y Literatura
Tecnología
Filosofía
Varios
Historia
Historia del Arte, Humanidades, Historia, Historia Contemporánea, Prehistoria...
leer másCiencias y Matemáticas
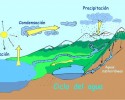
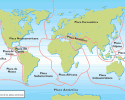
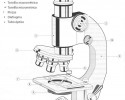
Biología, Física, Química, Geografía, Ciencias Políticas, Ciencias de la Salud...
leer másTecnologia
Tecnología de la información, Tecnología industrial, Electrónica...
leer másFilosofía
Ética, Psicopedagogía, Sociología, Antropología, Lógica, Metafísica, Conocimiento...
leer másBásico
Matemáticas, Religión, Ciencias naturales, Ciencias sociales, Educación artística, Arte y dibujo...
leer másVarios
Actividad física, Educación para la ciudadanía, Economía, Fundamentos de derecho, Música...
leer másLengua y Literatura
Lingüistica, Filología, Lengua Española, Literatura Española, Etimología, Morfología, Ortografía...
leer más